
Decision trees are one of the most common tools in a data analyst’s machine learning toolkit. In this guide, you’ll learn what decision trees are, how they are built, various applications, benefits, and more.
Table of contents
What is a decision tree?
In machine learning (ML), a decision tree is a supervised learning algorithm that resembles a flowchart or decision chart. Unlike many other supervised learning algorithms, decision trees can be used for both classification and regression tasks. Data scientists and analysts often use decision trees when exploring new datasets because they are easy to construct and interpret. Additionally, decision trees can help identify important data features that may be useful when applying more complex ML algorithms.
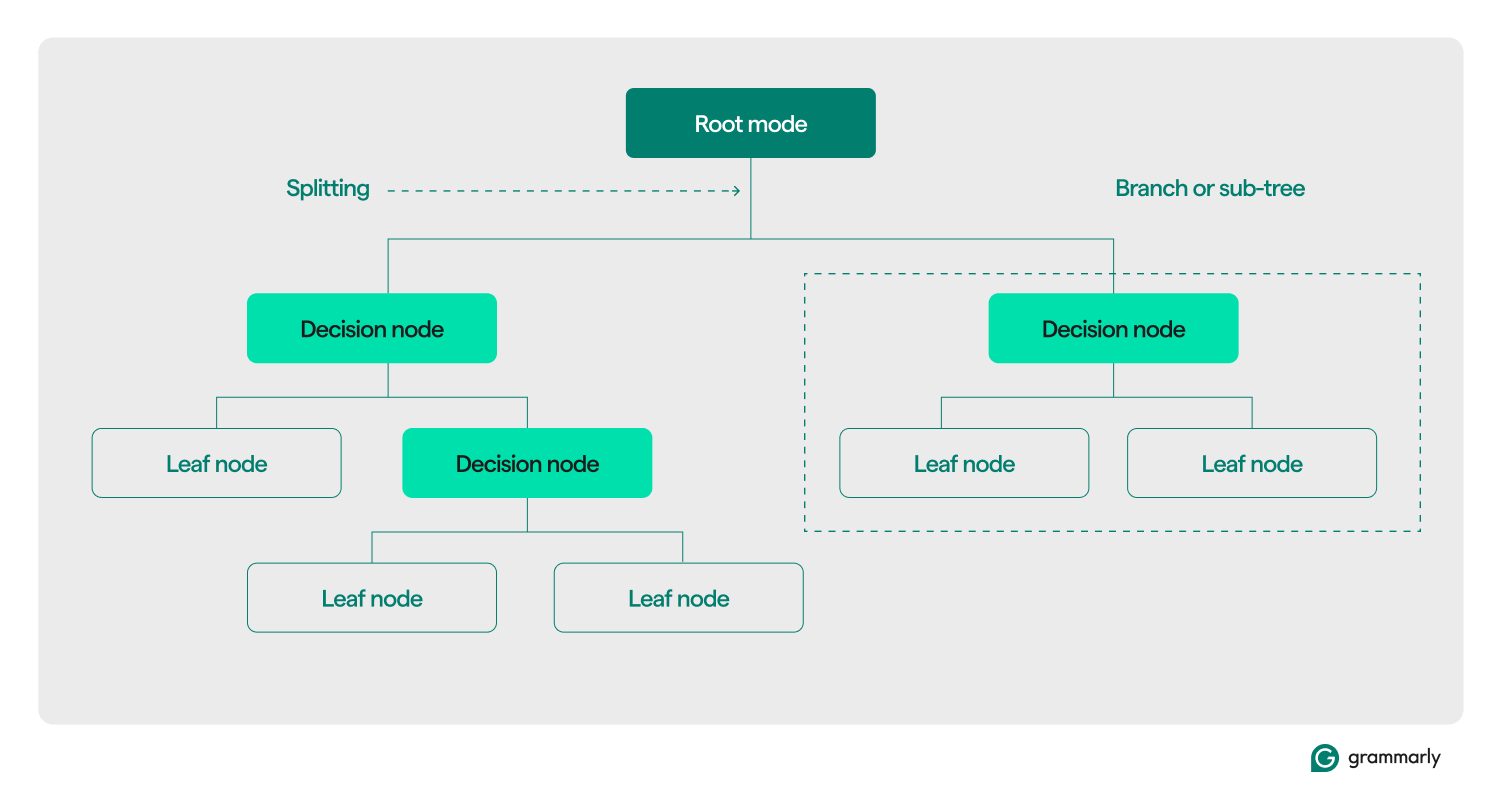
Decision tree terminology
Structurally, a decision tree typically consists of three components: a root node, leaf nodes, and decision (or internal) nodes. Just like flowcharts or trees in other domains, decisions in a tree usually move in one direction (either down or up), starting from the root node, passing through some decision nodes, and ending at a specific leaf node. Each leaf node connects a subset of the training data to a label. The tree is assembled through an ML training and optimization process, and once built, it can be applied to various datasets.
Here’s a deeper dive into the rest of the terminology:
- Root node: A node holding the first of a series of questions that the decision tree will ask about the data. The node will be connected to at least one (but usually two or more) decision or leaf nodes.
- Decision nodes (or internal nodes): Additional nodes containing questions. A decision node will contain exactly one question about the data and direct the dataflow to one of its children based on the response.
- Children: One or more nodes that a root or decision node points to. They represent a list of next options that the decision-making process can take as it analyzes data.
- Leaf nodes (or terminal nodes): Nodes that indicate the decision process has been completed. Once the decision process reaches a leaf node, it will return the value(s) from the leaf node as its output.
- Label (class, category): Generally, a string associated by a leaf node with some of the training data. For example, a leaf might associate the label “Satisfied customer” with a set of specific customers that the decision tree ML training algorithm was presented with.
- Branch (or sub-tree): This is the set of nodes consisting of a decision node at any point in the tree, together with all of its children and their children, all the way down to the leaf nodes.
- Pruning: An optimization operation typically performed on the tree to make it smaller and help it return outputs faster. Pruning usually refers to “post-pruning,” which involves algorithmically removing nodes or branches after the ML training process has built the tree. “Pre-pruning” refers to setting an arbitrary limit on how deep or large a decision tree can grow during training. Both processes enforce a maximum complexity for the decision tree, usually measured by its maximum depth or height. Less common optimizations include limiting the maximum number of decision nodes or leaf nodes.
- Splitting: The core transformation step performed on a decision tree during training. It involves dividing a root or decision node into two or more sub-nodes.
- Classification: An ML algorithm that attempts to figure out which (out of a constant and discrete list of classes, categories, or labels) is the most likely one to apply to a piece of data. It might attempt to answer questions like “Which day of the week is best for booking a flight?” More on classification below.
- Regression: An ML algorithm that attempts to predict a continuous value, which may not always have bounds. It might attempt to answer (or predict the answer) to questions like “How many people are likely to book a flight next Tuesday?” We’ll talk more about regression trees in the next section.
Types of decision trees
Decision trees are typically grouped into two categories: classification trees and regression trees. A specific tree may be built to apply to classification, regression, or both use cases. Most modern decision trees use the CART (Classification and Regression Trees) algorithm, which can perform both types of tasks.
Classification trees
Classification trees, the most common type of decision tree, attempt to solve a classification problem. From a list of possible answers to a question (often as simple as “yes” or “no”), a classification tree will choose the most likely one after asking some questions about the data it’s presented with. They are usually implemented as binary trees, meaning each decision node has exactly two children.
Classification trees might try to answer multiple-choice questions such as “Is this customer satisfied?” or “Which physical store is likely to be visited by this client?” or “Will tomorrow be a good day to go to the golf course?”
The two most common methods to measure the quality of a classification tree are based on information gain and entropy:
- Information gain: The efficiency of a tree is enhanced when it asks fewer questions before reaching an answer. Information gain measures how “quickly” a tree can achieve an answer by evaluating how much more information is learned about a piece of data at each decision node. It assesses whether the most important and useful questions are asked first in the tree.
- Entropy: Accuracy is crucial for decision tree labels. Entropy metrics measure this accuracy by evaluating the labels produced by the tree. They assess how often a random piece of data ends up with the wrong label and the similarity among all pieces of training data that receive the same label.
More advanced measurements of tree quality include the gini index, gain ratio, chi-square evaluations, and various measurements for variance reduction.
Regression trees
Regression trees are typically used in regression analysis for advanced statistical analysis or to predict data from a continuous, potentially unbounded range. Given a range of continuous options (e.g., zero to infinity on the real number scale), the regression tree attempts to predict the most likely match for a given piece of data after asking a series of questions. Each question narrows down the potential range of answers. For instance, a regression tree might be used to predict credit scores, revenue from a line of business, or the number of interactions on a marketing video.
The accuracy of regression trees is usually evaluated using metrics such as mean square error or mean absolute error, which calculate how far off a specific set of predictions is compared to the actual values.
How decision trees work
As an example of supervised learning, decision trees rely on well-formatted data for training. The source data usually contains a list of values that the model should learn to predict or classify. Each value should have an attached label and a list of associated features—properties the model should learn to associate with the label.
Building or training
During the training process, decision nodes in the decision tree are recursively split into more specific nodes according to one or more training algorithms. A human-level description of the process might look like this:
- Start with the root node connected to the entire training set.
- Split the root node: Using a statistical approach, assign a decision to the root node based on one of the data features and distribute the training data to at least two separate leaf nodes, connected as children to the root.
- Recursively apply step two to each of the children, turning them from leaf nodes into decision nodes. Stop when some limit is reached (e.g., the height/depth of the tree, a measure of the quality of children in each leaf at each node, etc.) or if you’ve run out of data (i.e., each leaf contains data points that are related to exactly one label).
The decision of which features to consider at each node differs for classification, regression, and combined classification and regression use cases. There are many algorithms to choose from for each scenario. Typical algorithms include:
- ID3 (classification): Optimizes entropy and information gain
- C4.5 (classification): A more complex version of ID3, adding normalization to information gain
- CART (classification/regression): “Classification and regression tree”; a greedy algorithm that optimizes for minimum impurity in result sets
- CHAID (classification/regression): “Chi-square automatic interaction detection”; uses chi-squared measurements instead of entropy and information gain
- MARS (classification/regression): Uses piecewise linear approximations to capture non-linearities
A common training regime is the random forest. A random forest, or a random decision forest, is a system that builds many related decision trees. Multiple versions of a tree might be trained in parallel using combinations of training algorithms. Based on various measurements of tree quality, a subset of these trees will be used to produce an answer. For classification use cases, the class selected by the largest number of trees is returned as the answer. For regression use cases, the answer is aggregated, usually as the mean or average prediction of individual trees.
Evaluating and using decision trees
Once a decision tree has been constructed, it can classify new data or predict values for a specific use case. It’s important to keep metrics on tree performance and use them to evaluate accuracy and error frequency. If the model deviates too far from expected performance, it might be time to retrain it on new data or find other ML systems to apply to that use case.
Applications of decision trees in ML
Decision trees have a wide range of applications in various fields. Here are some examples to illustrate their versatility:
Informed personal decision-making
An individual might keep track of data about, say, the restaurants they’ve been visiting. They might track any relevant details—such as travel time, wait time, cuisine offered, opening hours, average review score, cost, and most recent visit, coupled with a satisfaction score for the individual’s visit to that restaurant. A decision tree can be trained on this data to predict the likely satisfaction score for a new restaurant.
Calculate probabilities around customer behavior
Customer support systems might use decision trees to predict or classify customer satisfaction. A decision tree can be trained to predict customer satisfaction based on various factors, such as whether the customer contacted support or made a repeat purchase or based on actions performed within an app. Additionally, it can incorporate results from satisfaction surveys or other customer feedback.
Help inform business decisions
For certain business decisions with a wealth of historical data, a decision tree can provide estimates or predictions for the next steps. For example, a business that collects demographic and geographic information about its customers can train a decision tree to evaluate which new geographic locations are likely to be profitable or should be avoided. Decision trees can also help determine the best classification boundaries for existing demographic data, such as identifying age ranges to consider separately when grouping customers.
Feature selection for advanced ML and other use cases
Decision tree structures are human readable and understandable. Once a tree is built, it is possible to identify which features are most relevant to the dataset and in what order. This information can guide the development of more complex ML systems or decision algorithms. For instance, if a business learns from a decision tree that customers prioritize the cost of a product above all else, it can focus more complex ML systems on this insight or ignore cost when exploring more nuanced features.
Advantages of decision trees in ML
Decision trees offer several significant advantages that make them a popular choice in ML applications. Here are some key benefits:
Quick and easy to build
Decision trees are one of the most mature and well-understood ML algorithms. They don’t depend on particularly complex calculations, and they can be built quickly and easily. As long as the information required is readily available, a decision tree is an easy first step to take when considering ML solutions to a problem.
Easy for humans to understand
The output from decision trees is particularly easy to read and interpret. The graphical representation of a decision tree doesn’t depend on an advanced understanding of statistics. As such, decision trees and their representations can be used to interpret, explain, and support the results of more complex analyses. Decision trees are excellent at finding and highlighting some of the high-level properties of a given dataset.
Minimal data processing required
Decision trees can be built just as easily on incomplete data or data with outliers included. Given data decorated with interesting features, the decision tree algorithms tend not to be affected as much as other ML algorithms if they are fed data that hasn’t been preprocessed.
Disadvantages of decision trees in ML
While decision trees offer many benefits, they also come with several drawbacks:
Susceptible to overfitting
Decision trees are prone to overfitting, which occurs when a model learns the noise and details in the training data, reducing its performance on new data. For example, if the training data is incomplete or sparse, small changes in the data can produce significantly different tree structures. Advanced techniques like pruning or setting a maximum depth can improve tree behavior. In practice, decision trees often need updating with new information, which can significantly alter their structure.
Poor scalability
In addition to their tendency to overfit, decision trees struggle with more advanced problems that require significantly more data. Compared to other algorithms, the training time for decision trees increases rapidly as data volumes grow. For larger datasets that might have significant high-level properties to detect, decision trees are not a great fit.
Not as effective for regression or continuous use cases
Decision trees don’t learn complex data distributions very well. They split the feature space along lines that are easy to understand but mathematically simple. For complex problems where outliers are relevant, regression, and continuous use cases, this often translates into much poorer performance than other ML models and techniques.